前回は標準のReLightNodeを用いて、Relightingを行いました。ただ、このRelightingの結果を直接add mixなどでのせても味気ないので、もう一味つけるためにもReflection Mappingを施したいと思います。
Reflection Mappingに関しては、以前も一度投稿してます。 PworlrdとNworldとカメラの情報さえあれば、Nukeの中でReflection Mappingができちゃいます。やり方は、OpenGLなどでは、割と有名は方法らしいのですが(OpenGLの大家の床井先生も紹介されていました)、LTEの藤田さんに、ものすごく丁寧にご教授いただきました。その内容を説明したいとおもいます。
※注意 バカ丁寧に細かく説明しているので、長ったらしい内容になってますが、ヨクヨク読めば、たいしたないようではありません。根気よく読んでもらえればと。
原理的には、ジオメトリ上の任意の点にカメラからみてどちらの方向へ反射するかで、さらに、その反射を球体マッピング的な環境で出してしまおうという感じです。
カメラからの視線を入射角として、その視線が当たる点の法線から反射角を求め、さらにそれをuv mappingに置き換えるという手法です。
まずは、 カメラの位置とPworldから、視線ベクトル(入射角)を求めます。
Pworldは、平たく言えば各ピクセルの位置情報です。当然座標なんて本来8bitの色情報である0-255に収まらないのですが、ダイナミックレンジを格納できるOpenEXRならでは利点で0-255をプラスにもマイナスにも超えて格納してしまいます。
たとえば、上記のように、 といった感じで、8bitのRGBはNuke上では0-1でなのですが、それに縛られない数値になっていることが確認できます。Pworldではそれを利用して、RGB = XYZ として位置情報が格納されています。
それを用いて、カメラ位置を "C" としPworldを "P" とし 視線ベクトルを "E" とすると
E = normalize( P - C )
で求めることができます。
"normalize" というのは、ベクトルの長さを "1" にするという処理です。
この後法線ベクトル(Nworld)を用いて反射ベクトルを求めるために必須事項です。乱暴な解釈ですが、諸々ベクトルの長さを "1" で計算してやれば、結果、反射ベクトルの長さが一定になり、さらに、そうすると、任意のピクセルでの反射ベクトルはその一定の長さを半径としたの「球面」上のドコカシロに終点があることになり、球面マッピングの手法でReflectionが求められます。間違ってたらごめんなさい・・・
で、じゃあ、肝心のどうやってそれをNuke上で表現するかですが・・・
RGBの計算を行えるように一旦カメラ位置 "C" をExpressionNodeを用いてRGBに格納します。
Expressionを用いれば、数式はある程度まとめて、NodeOperatorの数を減らすことができるのですが、今回はわかりやすさを目指して、まわりくどく細かくNodeにわけていくことにします。
で、カメラノードの名前がcamera1として、
C = (Cx,Cy,Cz) = ((Camera1.translate.x),(Camera1.translate.y),(Camera1.translate.z))
として、これをRGBに格納します。
こんな感じで。ExpressionNodeを用いています。
で、さらに、MergeExpressionNodeを用いて、"P - C" を求めます。MergeExpressionNodeを用いると2個のインプットに対してRGBの計算を各ピクセルで行うことができます。
MergeExpressionでrgbで計算をするため、一旦Pworldをrgbに変換します。
P - C = (Px,Py,Pz) - (Cx,Cy,Cz) = ( ( Px - Cx ) , ( Py - Cy ) , ( Pz - Cz ) )
となり、Nuke上ではx,y,zをR,G,Bとして扱っており、さらに、MergeExpressionではinputがAとBとあり、それぞれのベクトルは (Ar,Ag,Ab)、(Br,Bg,Bb) であらわされます。
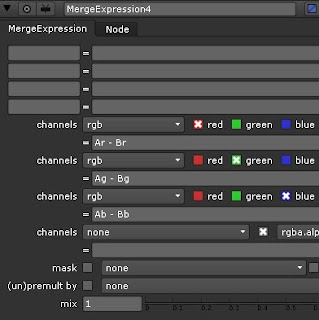
なので、inputAをPworld、inputBをカメラ位置 "C"とすると、MergeExpression上で
P - C = ( ( Ar - Br ) , ( Ag - Bg ) , ( Ab - Bb ) )
で示せて、実際には
さらに上で求められた、"P - C" のベクトルの長さ(length)を
length = sqrt( (P - C)x*(P - C)x + (P - C)y*(P - C)y + (P - C)y*(P - C)y )
で求めます。長さはベクトルの各成分(x,y,z)の2乗の和の平方根( √ = sqrt( ) )ですので、上の式がそれそのものです。 これをExpressionNodeに落とし込むと、
length = sqrt((r*r)+(g*g)+(b*b))
となり、視線ベクトル "E" は、"P - C" の各成分を、上記で求めた自身の長さ "length" で割ったものなので、
E = normalize( P - C ) = ( r/length , g/length , b/length, ) となり、
となり、長さ "1" のベクトルである視線ベクトル "E" が求められます。
この 長さを "1" にすることを "normalize" と呼んだり、正規化と呼んだりするようです。
ちなみに、RGB値の(この場合ベクトルでのxyzの)四足混合の一つずつだけなら、ExpressionNodeを使わずにMergeNodeの "add" "minus" "multiply" "divide" でも出来ます。順序はA operation Bのようです。minusなら A-Bの順序で組むことが可能です。
さらに、視線ベクトル "E" から反射ベクトル(反射角)を求めます。ここで、反射ベクトルを "R" 、法線ベクトル(Nworld)を "N" とし、反射ベクトル "R" はベクトルの内積を用いて次の公式で与えられます。
R = E - ( 2*(E.N)*N )
"E.N" は、視線ベクトル "E" と 法線ベクトル "N"の内積です。
内積の公式をもちいて、
E.N = (Ex*Nx)+(Ey*Ny)+(Ez*Nz)
とあらわすことができます。
さらに、これをMergeExpressionNodeに落とし込みます。どちらでも結果は同じですが、inputAを視線ベクトル "E" 、inputBを法線ベクトル "N とすると、
E.N = (Ar*Br)+(Ag*Bg)+(Ab*Bb)
であわらすことができ 、都合がいいように実際にShuffleNodeでNworldをRGBに変換しておき、MergeExpressionNodeを用いて・・・
こんな感じです。で、ひとまず
R = E - ( 2*(E.N)*N )
の残り部分 " 2*(E.N)*N " 部分までを求めてみます。MergeExpressionNodeを用いて、以下のようになります。
こんな感じで、さらに
R = E - ( 2*(E.N)*N )
の残り部分、上記で求めたものを視線ベクトル "E"から引きます。
MergeExpressionNodeを用いてもできますし、mergeのoperationを"minus"でもできます。
と、結果、これが、反射ベクトル "R" となります。
ココまで説明してきたように、MergeExpressionNodeは二つのNodeに対応しており、その二つのNode(AとB)に対して計算式を与えることができます。
で、先にも説明したように、画像上のどこのピクセルをとっても、この反射ベクトルの長さは一定なので、環境を「球面」とみなして、環境反射は反射ベクトルをもって、その球面上のある点を指定できます。実際には、計算などが扱い易いように、反射ベクトルも正規化しておきます。そうすることによって、球面上では任意の点[x,y,z]を、次の式を用いて、緯度経度座標[theata phi]に置き換えることができます。
theta = acos(-R.y)
phi = atan2(R.z,R.x) + PI
北緯○○度 東経○○度を思い浮かべてもらえばわかりやすいかもです。
ベクトルを、球体の中心からみて、それらの赤道方向の角度と北極南極を結ぶ線上をあらわす角度で表しています。
ここでのR.x、R.y、R.zは反射ベクトル "R" のそれぞれ x、y、z成分を指してます。PIは円周率です。
今までと同様にExpressionNodeでこれを表わすと
こんな感じです。
さらに、この球体(環境)の座標をuv座標(column(列)とrow(行))で考えて、0-1の範囲で表すと、
赤道方向(phi)は360度分の何度か、北極南極を結ぶ線上(theta)は180度分の何度かであらわせるので、
u = phi / (2*PI)
v = theta / PI
となりますので、
こんな感じです。
で反射ベクトルから環境を参照するためのuv座標を得ることができたので、それとSTMapNodeと環境用のマッピング画像を用いて
こんな感じで、Reflection MappingをNukeで実装できます。
ちなみに、STMapNodeはuv座標から指定したマップ(ここでは環境マップ)をルックアップしてやるためのNodeです。たとえば、
この点は r,g 成分は(0.31323 , 0.57227 )なので、マップからuv座標(column(列)とrow(行))値の(0.31323 , 0.57227 )を参照してきます。
こんな感じです。
入射角に対して、反射角の評価の仕方などを法線とあらかじめ用意したUVなどをくみあわせて、うまくいじってやれば、異方向性反射なども実装できると思います。
今回は環境マッピングでしたが、考え方はshadingにちかいので、NukeではPhong shaderしかありませんが、いろいろとカスタマイズすることも可能です。
もう少し続きますが、今回はココまで。






















No comments:
Post a Comment